超材料是由已知材料按特定排列方式组成的人造材料组合，能展现出天然材料所不具备的新奇特性。在众多应用领域中，超材料在隔振、噪声控制、波导以及能量收集技术等方面前景广阔。
尽管超材料研究的基石通常在于其周期性设计，但目前研究正拓展至准周期超材料领域，其缺乏平移周期性的特点为该领域带来了新的挑战与机遇。在本研究中，我们使用可重构的乐高积木和激光多普勒测振技术，来展示准周期材料的独特性质，包括局域振动模式和定向波工程特性。
在超材料研究中，谐振器被广泛用于构建所谓的 “局域共振” 超材料。通常，将相同的谐振器阵列附着在弹性结构上。这会产生带隙，即弹性波传播被禁止的频率波段，从而在附着物的共振频率附近降低整体振动水平。
许多研究团队都在探索这一思路，期望借此开发出隔振和隔音材料。该领域的经典理论是基于由等间距且调谐至相同频率的谐振器构成的周期性结构发展而来的。近年来，研究人员的兴趣逐渐超越周期性结构，开始探索无序和准周期谐振器阵列的特性。
本次实验中，我们将乐高积木用作机械谐振器的简易模型（图 1）。每个谐振器由一根支柱（黑色）和一个圆锥体（蓝色）组成。通过在支柱上滑动圆锥体，可以将谐振频率在约 200 - 350 Hz的范围内进行调节（如图1所示）。
这些谐振器以准周期配置附着在乐高横梁上，旨在改变其波传播和振动特性。实验中使用电动激振器作为样品振动激励，同时采用 Polytec 公司的扫描式激光多普勒测振仪（SLDV）记录样品平面（无谐振器一侧）的频率响应。
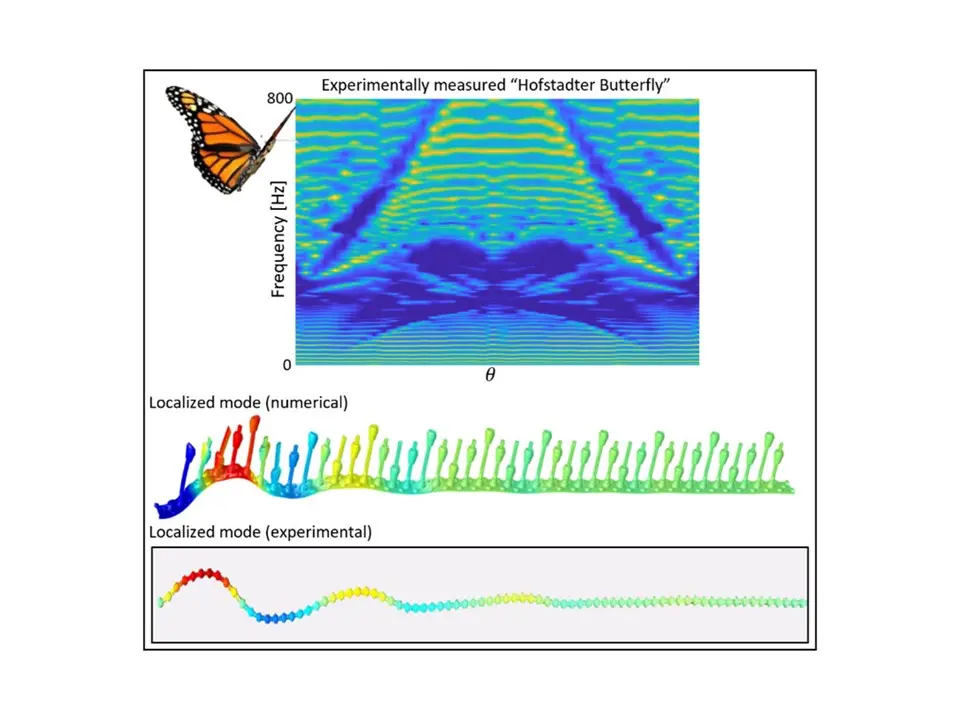
在第一项工作中，我们研究了附着有准周期谐振器阵列的一维弹性横梁 [1]。总共 42 个谐振器被安装在乐高横梁上，其高度按照准周期模式设定。具体而言，第 n 个谐振器的高度 hn由公式 hn = h0 + Δh sin (2πθn) 确定，由平均高度 h0 加上幅值为 Δh、波长为 1/θ 的正弦调制项构成。θ 参数的变化会产生一系列不同的模式；当 θ 为有理数时，对应周期性模式；当 θ 为无理数时，则对应准周期模式。
通过重新配置样品并进行一系列实验，我们能够获取频率响应随 θ 的变化情况。实验结果以彩色图的形式总结在图 2 中，颜色表示沿横梁跨度方向平均的响应，其为 θ（x 轴）和频率（y 轴）的函数。图中，黄色线条标记了与梁的共振相关的响应峰值变化，而蓝色区域则表示导致梁上振动水平较低的带隙。值得注意的是，该图形成了一个类似于霍夫施塔特蝴蝶的频谱图（因此配有蝴蝶图像）。
最初的霍夫施塔特蝴蝶指的是 20 世纪 80 年代道格拉斯・霍夫施塔特发现的，在强磁场作用下电子的分形频谱，它与量子霍尔效应理论相关。有趣的是，我们的实验通过使用可重构的弹性谐振器，而非具有磁场的电子系统，再现了类似的特征。这种惊人的相似性促使我们的研究成果发表在《应用物理快报》杂志上 [1]。
由于样品尺寸有限，我们自然只能捕捉到 “分形” 频谱的部分特征。量子霍尔效应的一个显著标志是 “边缘态” 的出现，即电流仅在样品边缘传播，而不通过内部。类似地，在我们的弹性实验平台中，这一特征表现为振动模态分布在横梁边缘。图 2 展示了一个频率约为 450 Hz的局部模态，并将有限元分析（FEA）数值结果和测振仪测量的试验模态振型进行了对比。
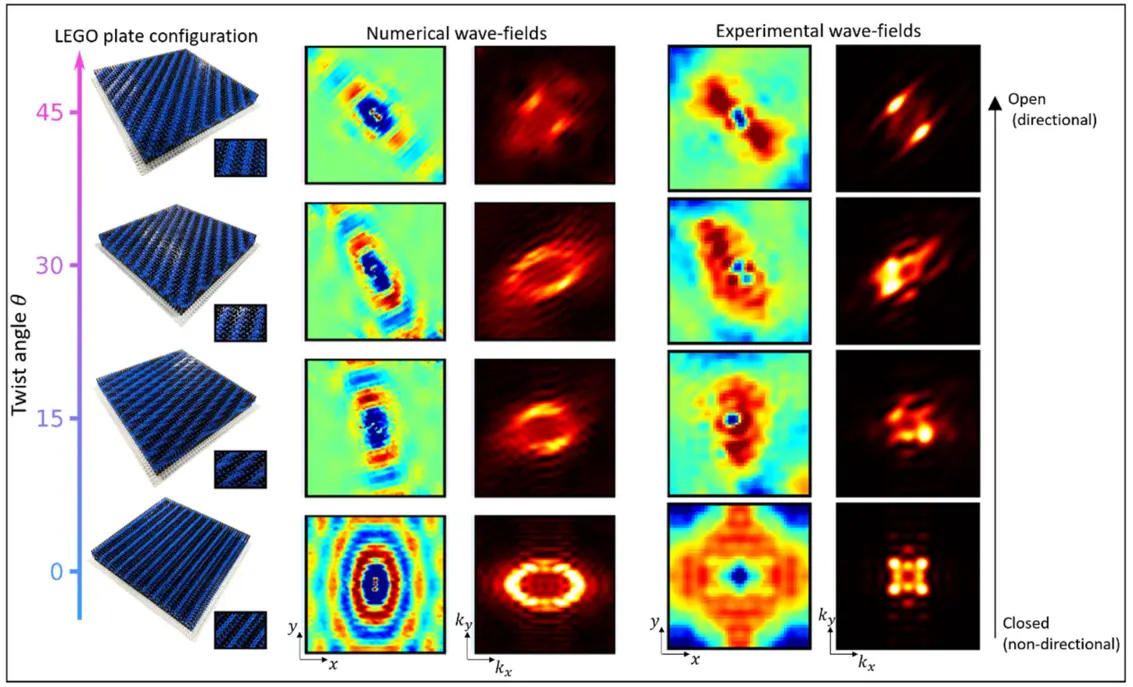
受上述发现的启发，我们继续探索附着在平板上的二维乐高正方形晶格的特性 [2]。通过对支柱高度进行正弦调制来获得准周期模式。此时， θ是正弦调制后支柱间的扭转角。
我们选择通过扭转实现准周期性，这一思路源于扭转双层电子系统，该系统展现出电子超导性等显著特性。在此，我们试图探究调制函数的扭转角（其会导致支柱高度形成不同的莫尔图案）如何改变乐高板内的弹性波传播。我们发现，加入乐高谐振器后，在特定频率下，板内的波传播具有高度方向性，并且扭转角的变化能够显著控制这一特性。
具体而言，扭转角会根据频率引发波传播从定向到非定向（或反之）的转变。图 3 展示了频率为 430 Hz时的一个例子，其中给出了扭转角为 0°、15°、30° 和 45° 时的数值结果，并与实验结果进行了对比。
在未扭转的情况下（θ = 0），板内的波传播不具有方向性，其波前呈椭圆形。因此，倒易空间的波场，是波数 kx、ky （波数通过傅里叶变换得到）的函数，其形状为封闭的椭圆轮廓。随着扭转角的增大和支柱的重新配置，在该固定频率下，波轮廓会打开并转变为 “双曲线” 轮廓，此时波具有高度的方向性。
此外，波的传播方向会随着扭转角扭转。由于波轮廓会根据波传播从非定向到定向的转变，从封闭形状变为开放形状，这种转变被称为拓扑转变。我们发表在《先进科学》杂志上的研究文章中还报道了许多其它示例 [2]。
通过乐高积木这一简单实验平台，我们通过试验展示了准周期超材料的卓越特性。这些特性受量子物质概念的启发，当应用于弹性材料时，会产生非传统的波的定位和波导特性。乐高实验平台的简易性使我们能够在桌面实验环境中研究这些复杂现象。展望未来，本研究展示的概念可应用于更复杂的超材料设计中，融入准周期图案，有望开发出具有卓越振动和波传播特性的新型材料。
References
[1] Rosa, M. I., Guo, Y., & Ruzzene, M. (2021). Exploring topology of 1D quasiperiodic metastructures through modulated LEGO resonators. Applied Physics Letters, 118(13), 131901.
https://aip.scitation.org/doi/full/10.1063/5.0042294
[2] Yves, S., Rosa, M. I. N., Guo, Y., Gupta, M., Ruzzene, M., & Alù, A. (2022). Moiré‐Driven Topological Transitions and Extreme Anisotropy in Elastic Metasurfaces. Advanced Science, 9(13), 2200181.
https://onlinelibrary.wiley.com/doi/full/10.1002/advs.202200181
Images courtesy of the authors unless otherwise specified. Cover image: Gts/shutterstock.com
