Metamaterials are artificial assemblies of known materials in particular arrangements that result in novel properties not encountered in naturally occurring materials. Among many applications, they hold great promise for vibration insulation, noise control, wave-guiding and energy harvesting technologies. While the cornerstone of metamaterials research usually lies in their periodic designs, research is currently expanding into the realm of quasi-periodic metamaterials, where the lack of translational periodicity poses new challenges and opportunities. In our work we use reconfigurable LEGO pieces and laser Doppler vibrometry to illustrate the unconventional features of quasi-periodic materials, including localized vibration modes and directional wave-engineering.
In metamaterials research, resonators are widely employed to compose the so-called “locally-resonant” metamaterials. Usually, arrays of identical resonators are attached to an elastic structure. This leads to the emergence of band gaps, which are frequency bands where elastic wave propagation is forbidden, resulting in an overall reduction in vibration levels around the resonance frequency of the attachments.
Multiple research groups explore this idea as an attractive route towards vibration and sound insulating materials. The classical theory in this area is developed based on periodic configurations composed of equally spaced resonators tuned to the same frequency. Recently, there is interest on going beyond periodic configurations, and exploring the properties of disordered and quasi-periodic resonator arrays.

Our experiments leverage LEGO pieces as simple implementations of mechanical resonators (Fig. 1). Each resonator is composed of a pillar (black) and a cone (blue). By sliding the cone along the pillar, the resonance frequency is tuned between a minimum and a maximum value of about 200 - 350 Hz (as illustrated in Fig. 1). These resonators are attached to a base LEGO beam or plate, in quasi-periodic configurations designed to alter their wave propagation and vibration features. An electrodynamic shaker is used to induce vibrations of the samples, while a Scanning laser Doppler vibrometer (SLDV) from Polytec is used to record the frequency response along the flat surface of the samples (the side without resonators).
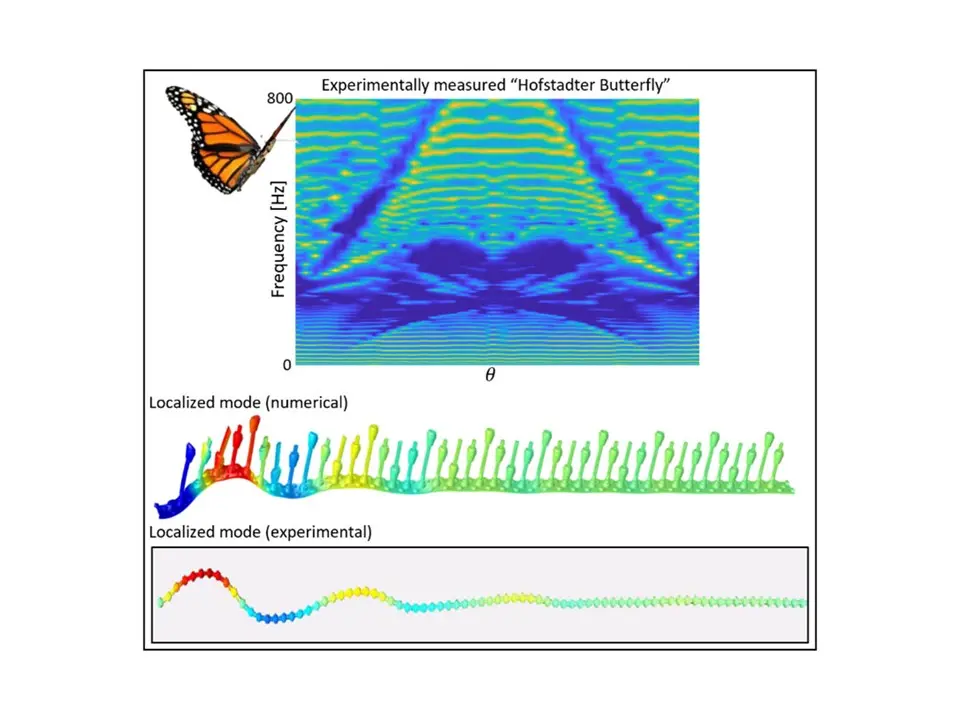
In the first work, we investigated one-dimensional elastic beams with quasi-periodic arrays of LEGO resonators [1]. A total of 42 resonators were attached to the LEGO beam, and their heights were assigned according to a quasi-periodic pattern. In particular, the height hn of the nth resonator is given by hn=h0+Δh sin(2πθn). It consists of a mean height h0, plus a sinusoidal modulation of amplitude Δh and wavelength 1/θ . Variation of the θ parameter results in a family of different patterns; rational θ values define periodic patterns, while irrational θ values define quasi-periodic patterns.
By reconfiguring our sample and performing a sequence of experiments, we were able to capture the variation of the frequency response as a function of θ . The results are summarized in Fig. 2 in the form of a colormap plot, with the color corresponding to the response averaged along the span of the beam as a function of θ (x axis) and frequency (y axis). In the figure, yellow lines mark the variation of the response peaks associated with the resonances of the beam, while blue regions are associated with bandgaps that result in low vibration levels across the beam. Notably, the picture forms a spectral map that resembles a Hofstadter Butterfly (hence the butterfly image).
The original butterfly refers to the fractal spectrum of electrons subject to a strong magnetic field, discovered in the 1980s by Douglas Hofstadter, and is related to the theory of the Quantum Hall Effect. Interestingly, our experiment reproduces similar features by using reconfigurable elastic resonators, rather than electronic systems with magnetic fields. This striking similarity motivated our featured publication in the Applied Physics Letters journal [1]. Naturally, we captured a small number of features of the “fractal” spectrum due to the limited size of our sample. One of the hallmarks of the Quantum Hall Effect is the appearance of “edge states”, which are currents that propagate only around the edge of a sample, and not through the interior.
Analogously, in our elastic platform, this feature manifests itself as vibration modes which are localized at the edges of the beam. An example of a localized mode at a frequency of about 450 Hz is illustrated in Fig. 2, with a comparison between the numerical result obtained through Finite Element Analysis (FEA) and the experimental mode shape measured by the vibrometer.
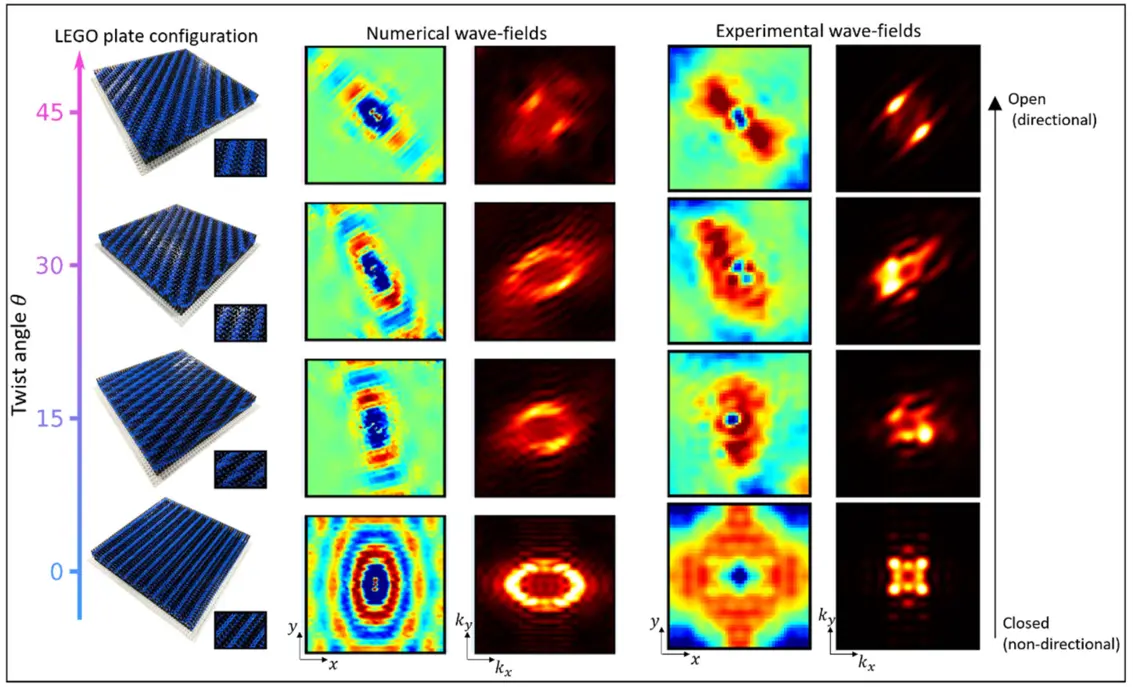
Excited by our findings, we continued to explore the features of a two-dimensional square lattice of LEGOs attached to a plate [2]. Quasi-periodic patterns are obtained by also using a sinusoidal modulation of the pillars’ heights. In this case, however, the relevant θ parameter is the twist angle between the sinusoidal modulation with respect to the pillars, which are fixed in space.
Our choice of quasi-periodicity through twisting was motivated by twisted bilayer electronic systems, which exhibit remarkable properties such as electronic superconductivity. Here, we sought to explore how the twist angle of the modulation function, which results in different configurations of the pillars heights forming moiré patterns, could alter the elastic wave propagation within the LEGO plate. We found that the inclusion of the LEGO resonators makes the wave propagation in the plate highly directional at specific frequencies, and the change in twist angle can provide remarkable control over this behavior.
In particular, the twist angle induces transitions between directional to non-directional wave propagation (or vice-versa), depending on the frequency. One example is illustrated in Fig. 3 for a frequency of 430 Hz, which illustrate numerical results and comparison with experimental results for twist angles of 0, 15, 30 and 45 degrees. In the untwisted case (θ=0) , wave propagation in the plate is not directional, and is characterized by oval wavefronts. Hence, the representation of the wave-field in reciprocal space as a function of wavenumbers kx,ky (obtained through Fourier Transformation) defines a closed elliptic contour. By increasing the twist angle and reconfiguring the pillars, the wave contours at that fixed frequency open and transform into “hyperbolic” contours, which define highly directional waves.
Furthermore, the direction of wave propagation is twisted according to the angle. This transition is called a topological transition since the wave contours change their shape from closed to open, according to the transition from non-directional to directional wave propagation. Multiple other examples are reported in our research article published in the Advanced Science journal [2].
Our findings exemplify remarkable properties of quasi-periodic metamaterials within a simple platform of LEGO pieces. The demonstrated properties are inspired by concepts of quantum matter, which when translated to elastic materials lead to unconventional wave localization and guiding features.
The simplicity of the LEGO implementation allows us to navigate these complex phenomena on table-top experimental platforms. Moving forward, the illustrated concepts can be translated into more complex metamaterial implementations that incorporate quasi-periodic patterns and may lead to novel materials with superior vibration and wave propagation features.








