Metamaterialien sind künstliche Gebilde bekannter Materialien, deren spezielle Anordnung neuartige Eigenschaften kreieren, die so in natürlichen Materialien nicht vorkommen. Neben vielen anderen Anwendungen bieten sie großes Potential hinsichtlich gezielter Schwingungsisolierung, der Lärmkontrolle, der Wellenleitung und der Energiegewinnung (Energy Harvesting). Während der Grundstein der Metamaterialforschung in der Regel im periodischen Design liegt, entwickelt sich die Forschung weiter in Richtung der quasi-periodischen Metamaterialien, wo das Fehlen der translatorischen Periodizität neue Herausforderungen und Möglichkeiten mit sich bringt. Diese Arbeit bedient sich rekonfigurierbaren LEGO-Bausteinen und deren Charakterisierung mit Laser-Doppler-Vibrometrie, um die unkonventionellen Eigenschaften quasi-periodischer Materialien zu veranschaulichen, einschließlich lokalisierter Schwingungsmoden und gerichteter Wellenentwicklung.
In der Metamaterialforschung werden häufig Resonatoren eingesetzt, um sogenannte "lokal-resonante" Metamaterialien zu bilden. In der Regel werden Arrays identischer Resonatoren an einer elastischen Struktur angebracht. Dadurch entstehen Bandlücken, d. h. Frequenzbänder, in denen die Ausbreitung elastischer Wellen unterdrückt ist, was in gewissen Bereichen zu einer Verringerung der Schwingungspegel um die Resonanzfrequenz führt.
Mehrere Forschungsgruppen untersuchen diese Idee als attraktiven Weg zu schwingungs- und schallisolierenden Materialien. Die klassische Theorie in diesem Bereich basiert auf periodischen Gebilden, die aus periodischen Resonatoren bestehen, die auf dieselbe Frequenz abgestimmt sind. In jüngster Zeit wächst das Interesse daran, über periodische Konfigurationen hinauszugehen und die Eigenschaften ungeordneter und quasi-periodischer Resonatoranordnungen zu erforschen.
In unseren Experimenten werden LEGO-Bausteine als vereinfachte mechanische Resonatoren (Abb. 1) verwendet. Jeder Resonator besteht aus einer Säule (schwarz) und einem Kegel (blau). Durch Verschieben des Kegels entlang der Säule wird die Resonanzfrequenz zwischen einem Minimal- und einem Maximalwert von etwa 200 - 350 Hz eingestellt (siehe Abb. 1). Diese Resonatoren sind in quasi-periodischen Konfigurationen an einem LEGO-Basisbalken oder einer Platte befestigt, um ihre Wellenausbreitung und Schwingungseigenschaften zu verändern. Ein elektrodynamischer Shaker dient der Probenanregung, während ein Scanning Laser-Doppler-Vibrometer (SLDV) von Polytec die Frequenzantwort entlang der flachen Oberfläche der Proben (die Seite ohne Resonatoren) aufzeichnet.
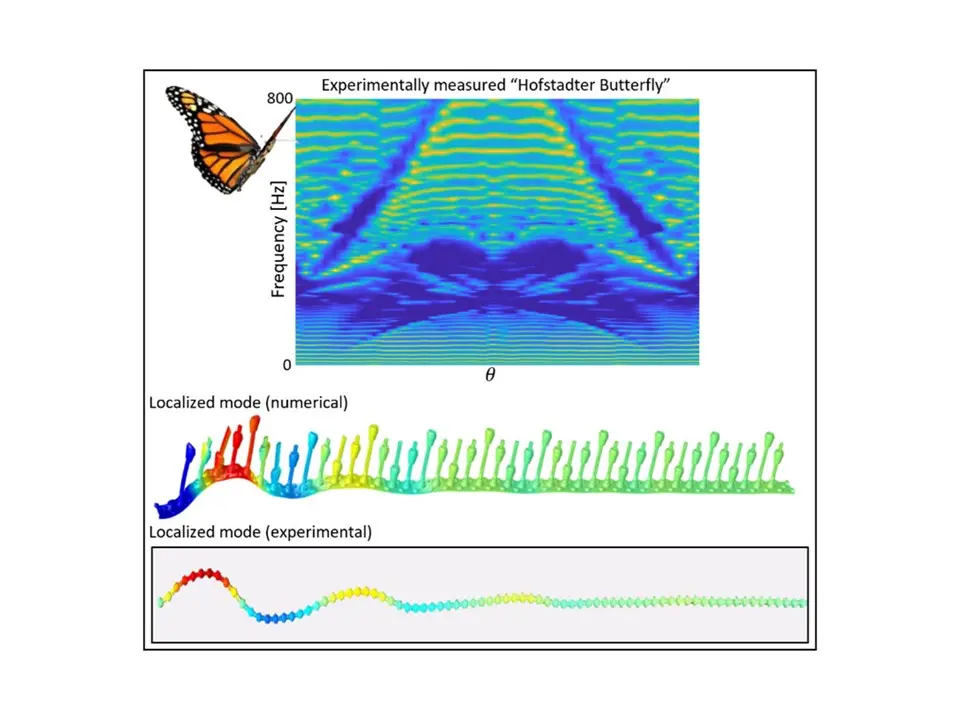
Im ersten Schritt untersuchten wir eindimensionale elastische Balken mit quasi-periodischen Anordnungen von LEGO-Resonatoren [1]. Insgesamt 42 Resonatoren sind an den LEGO-Balken angebracht, und die Kegelhöhe ist nach einem quasi-periodischen Muster zugewiesen. Im Einzelnen ist die Kegelhöhe hn des nth Resonators gegeben durch hn=h0+Δh sin(2πθn). Er besteht aus einer mittleren Höhe h0 und einer sinusförmigen Modulation der Amplitude Δh und der Wellenlänge 1/θ .
Die Variation des Parameters θ führt zu einer Familie verschiedener Muster; rationale θ-Werte definieren periodische Muster, während irrationale θ-Werte quasi-periodische Muster definieren. Die Ergebnisse sind in Abb. 2 in Form eines Farbdiagramms zusammengefasst, wobei die Farbe dem über die Spannweite des Strahls gemittelten Frequenzgang in Abhängigkeit von θ (x-Achse) und der Frequenz (y-Achse) entspricht. In der Abbildung markieren gelbe Linien die Variation der Antwortspitzen, die mit den Resonanzen des Balkens verbunden sind, während blaue Regionen mit Bandlücken verbunden sind, die zu niedrigen Schwingungspegeln über den Balken führen. Das Bild formt eine spektrale Karte, die einem Hofstadter Schmetterling ähnelt (daher das Schmetterlingsbild).
Der ursprüngliche Schmetterling bezieht sich auf das fraktale Spektrum von Elektronen, die einem starken Magnetfeld ausgesetzt sind, das in den 1980er Jahren von Douglas Hofstadter entdeckt wurde und mit der Theorie des Quanten-Hall-Effekts in Zusammenhang steht. Interessanterweise reproduziert unser Experiment ähnliche Eigenschaften, indem es vielmehr rekonfigurierbare elastische Resonatoren denn elektronische Systeme mit Magnetfeldern verwendet. Diese verblüffende Ähnlichkeit war der Grund für unsere Veröffentlichung in der Zeitschrift Applied Physics Letters [1]. Aufgrund der begrenzten Größe unserer Stichprobe wurde nur eine kleine Anzahl von Merkmalen des "fraktalen" Spektrums erfasst.
Eines der Markenzeichen des Quanten-Hall-Effekts ist das Auftreten von "Randzuständen", d. h. von Strömen, die sich nur am Rand einer Probe und nicht im Inneren ausbreiten. In unserer elastischen Plattform manifestiert sich diese Eigenschaft in Form von Schwingungsmoden, die an den Rändern des Strahls lokalisiert sind. Ein Beispiel für eine lokalisierte Schwingungsform bei einer Frequenz von etwa 450 Hz ist in Abb. 2 dargestellt, mit einem Vergleich zwischen dem numerischen Ergebnis der Finite-Elemente-Analyse (FEA) und der experimentellen Schwingungsform, die mit dem Vibrometer gemessen wurde.
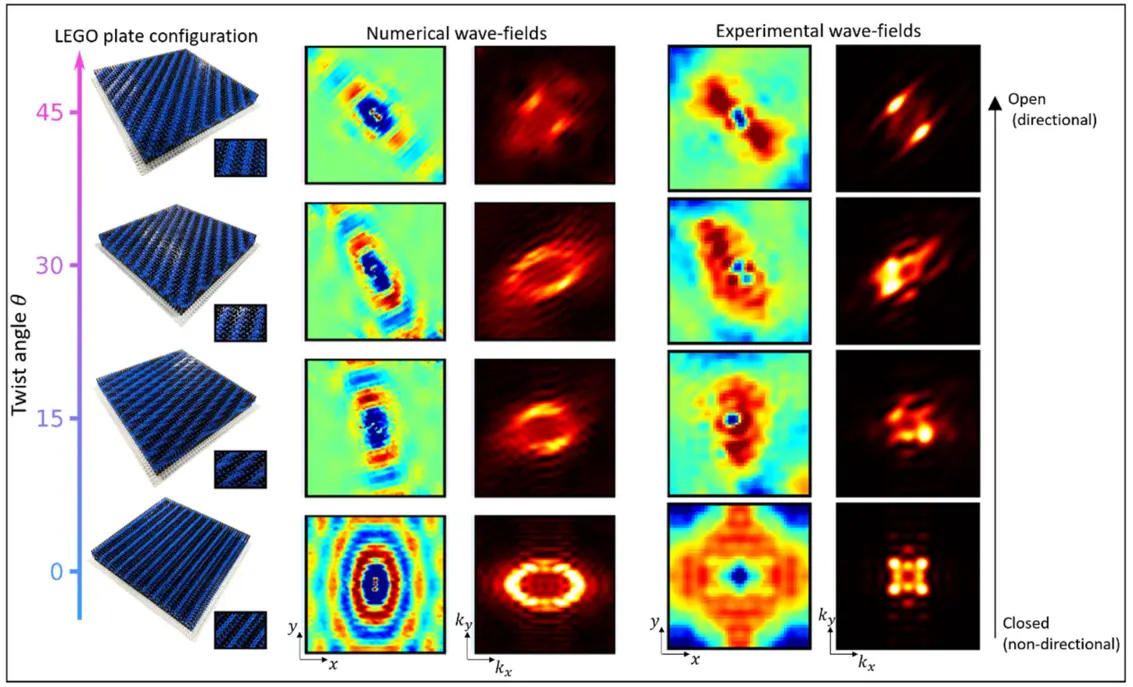
Angeregt durch unsere Erkenntnisse haben wir die Eigenschaften eines zweidimensionalen quadratischen Gitters aus LEGO, das auf einer Platte befestigt ist, weiter erforscht [2]. Quasi-periodische Muster erhält man auch durch eine sinusförmige Modulation der Säulenhöhen. In diesem Fall ist der relevante θ-Parameter jedoch der Verdrehungswinkel zwischen der sinusförmigen Modulation und den Säulen, die im Raum fixiert sind.
Unsere Wahl einer Quasiperiodizität durch Verdrehung wurde durch verdrehte elektronische Doppelschichtsysteme inspiriert, welche bemerkenswerte Eigenschaften wie z.B. eine elektronische Supraleitfähigkeit aufweisen. Hier wollten wir untersuchen, wie der Verdrehungswinkel der Modulationsfunktion, der zu unterschiedlichen Konfigurationen der Säulenhöhen führt, die Moiré-Muster bildet, die elastische Wellenausbreitung innerhalb der LEGO-Platte verändern könnte.
Wir fanden heraus, dass die Wellenausbreitung in der Platte durch die LEGO-Resonatoren bei bestimmten Frequenzen stark gerichtet ist und dass die Änderung des Verdrehungswinkels eine bemerkenswerte Kontrolle über dieses Verhalten ermöglicht. Insbesondere bewirkt der Verdrehungswinkel je nach Frequenz den Übergang von gerichteter zu ungerichteter Wellenausbreitung (oder umgekehrt). Ein Beispiel ist in Abb. 3 für eine Frequenz von 430 Hz dargestellt, die die numerischen Ergebnisse und den Vergleich mit experimentellen Ergebnissen für Verdrehungswinkel von 0, 15, 30 und 45 Grad zeigt. Im unverdrillten Fall (θ=0) ist die Wellenausbreitung in der Platte ungerichtet und durch ovale Wellenfronten gekennzeichnet. Daher definiert die Darstellung des Wellenfeldes im reziproken Raum als Funktion der Wellenzahlen kx, ky (durch Fourier-Transformation erhalten) eine geschlossene elliptische Kontur.
Durch Vergrößerung des Verdrehungswinkels und Neuanordnung der Säulen öffnen sich die Wellenkonturen bei dieser festen Frequenz und werden zu "hyperbolischen" Konturen, die stark gerichtete Wellen definieren. Außerdem wird die Richtung der Wellenausbreitung entsprechend dem Winkel verdreht. Dieser Übergang wird als topologischer Übergang bezeichnet, da die Wellenkonturen ihre Form entsprechend dem Übergang von ungerichteter zu gerichteter Wellenausbreitung von geschlossen zu offen ändern. Mehrere andere Beispiele sind in unserem Forschungsartikel in der Zeitschrift Advanced Science [2] veröffentlicht.
Unsere Ergebnisse zeigen bemerkenswerte Eigenschaften von quasi-periodischen Metamaterialien innerhalb einer einfachen Plattform aus LEGO-Steinen. Die gezeigten Eigenschaften sind von Konzepten der Quantenmaterie inspiriert, die, wenn sie auf elastische Materialien übertragen werden, zu unkonventioneller Wellenlokalisierung und -leitung führen. Die Einfachheit der LEGO-Implementierung ermöglicht es uns, diese komplexen Phänomene auf Tisch-Experimentierplattformen zu erforschen.
In Zukunft können die vorgestellten Konzepte auf komplexere Metamaterialien übertragen werden, die quasi-periodische Muster enthalten und zu neuartigen Materialien mit überlegenen Schwingungs- und Wellenausbreitungseigenschaften führen können.
Referenzen
[1] Rosa, M. I., Guo, Y., & Ruzzene, M. (2021). Exploring topology of 1D quasiperiodic metastructures through modulated LEGO resonators. Applied Physics Letters, 118(13), 131901.
https://aip.scitation.org/doi/full/10.1063/5.0042294
[2] Yves, S., Rosa, M. I. N., Guo, Y., Gupta, M., Ruzzene, M., & Alù, A. (2022). Moiré‐Driven Topological Transitions and Extreme Anisotropy in Elastic Metasurfaces. Advanced Science, 9(13), 2200181.
https://onlinelibrary.wiley.com/doi/full/10.1002/advs.202200181
Bildnachweise: Soweit nachfolgend nicht anders aufgeführt bei den Autoren. Titelbild: Gts/shutterstock.com
